排序

各个排序算法的复杂度以及稳定性

名称	类别	平均时间	最好时间	最坏时间	空间	稳定性
直接插入	插入	$n^2$	$n$	$n^2$	1	√
二分插入	插入	$n^2$	$n$	$n^2$	1	√
希尔排序	插入	$n^{1.3}$	$n$	$n^2$	1
直接选择	选择	$n^2$	$n^2$	$n^2$	1
堆排序	选择	$n\log n$	$n\log n$	$n \log n$	1
冒泡	交换	$n^2$	$n$	$n^2$	1	√
快速	交换	$n \log n$	$n\log n$	$n^2$	$\log n$
归并	-	$n \log n$	$n\log n$	$n \log n$	$n$	√
基数	-	$d(r+n)$	$d(n+rd)$	$d(r+n)$	$rd+n$	√

有很多办法可以将任意排序算法变成稳定的，但是，往往需要额外的时间或者空间。

为什么直接选择排序不稳定？

因为直接选择排序是原地排序，每次选最大的和当前排好的最后一个交换。

例如：(7) 2 5 9 3 4 [7] 1。排序的第一步就会将 (7) 和 1 进行调换，这样 (7) 就跑到了 [7] 的后面了。

为什么快排的空间复杂度是 $\log n$？

这是平均情况，最坏是 $n$，其复杂度主要来自于函数调用栈。因为快速排序本质上是一种递归排序算法。我们平均需要调用 $\log n$ 次。

为什么归并的空间复杂度是 $n$？

归并排序会用到临时数组来做归并。

基数排序和桶排序？

• 基数排序是一种桶排序。
• 基数排序将数按位进行切割。
• 基数排序不仅仅适用于整数。

计数排序？

• 要求必须是整数。
• 是稳定的。

为什么二分插入排序复杂度仍然是 $n^2$？

虽然比较的次数减少了，但是交换的次数并没有变少，找到位置之后还是需要对所有的元素进行移位。

快速排序

快速排序的 Python 实现：

def partition(arr, low, high):
    pivot, j = arr[low], low
    for i in range(low + 1, high + 1): 
        if arr[i] <= pivot:
            j += 1
            arr[j], arr[i] = arr[i], arr[j]
    arr[low], arr[j] = arr[j], arr[low]
    return j 

def quick_sort_between(arr: List[int], low: int, high: int):
    if high - low <= 1:
        return

    m = partition(arr, low, high)
    quick_sort_between(arr, low, m - 1)
    quick_sort_between(arr, m + 1, high)

诀窍在于：从左到右遍历，记录一个指针指向小于 pivot 的数组的最后一个位置，如果发现满足条件（小于 pivot）的就交换。其实就是找到所有比它小的然后放到前面的位置里。

归并排序

多路归并排序

是外排序的基础。

1. 假设有 K 路 数据流，流内部是有序的，且流间同为升序或降序；
2. 首先读取每个流的第一个数，如果已经 EOF，那么 Pass；
3. 将有效的 k ( k 可能小于 K ) 个数比较，选出最小的那路，输出，读取其下一个；
4. 直到所有 K 路都 EOF。

基数排序（Radix Sort）

桶排序和计数排序是比较类似的，只不过计数排序是一个数字一个桶，而桶排序是一个桶可以包含多个数字。

基数排序是稳定的，因为即使两个数是一样的，那么他们放入的顺序就是他们本来的顺序，同时取出的顺序也是这样。

基数排序和和上面两个都不一样。基数排序的基本理论如下：

1. 先找到最大值，看最大值有几位，有多少位就要进行多少轮；
2. 创建 10 个桶，每一个桶对应 0~9 中的一个数字；
3. 从数据的个位开始 (从最高位开始也可以，结果一样)，按个位数对数据进行分桶
4. 将所有桶中的数据进行合并，合并时按先进先出的原则取出桶中的数据。
5. 重复步骤 3、4，继续按其他位对前面处理过的数据进行分桶和合并。一直到对每一位数据都进行分桶和合并完成，最终得到一个有序序列，列表排序完成。

def radix_sort(array):
    max_num = max(array)
    place = 1

    # 找到最大的数有多少位数
    while max_num >= 10**place:
        place += 1

    # 根据位数，决定要跑多少轮
    for i in range(place):
        # 分桶
        buckets = [[] for _ in range(10)]
        for num in array:
            radix = int(num/(10**i) % 10)
            buckets[radix].append(num)

        # 将桶内的内容按序取出
        j = 0
        for k in range(10):
            for num in buckets[k]:
                array[j] = num
                j += 1
    return array

动态规划

动态规划的一般问题形式是求 最值，⽐如说让你求 最⻓递增⼦序列，最⼩编辑距离 等等。

动态规划解法其实是一种 穷举。但其实也可以不进行穷举，通过合理的安排来只计算需要得到的值。

动态规划三特性

动态规划问题有三个特性，分别是 重叠⼦问题、最优⼦结构、状态转移⽅程。

最优子结构

最优子结构指的是需要解决的子问题之间是 相互独立 的，也就是 只要知道子问题的最优解，那么总问题的解就能得到。也就是我们可以通过一些问题的最优解得到另一个问题的最优解，解整个大问题的过程就是找出所有最优解的过程，这个解过程的（树）结构是通过各个不同规模问题的最优解得到的，而与子问题的非最优解无关，所以我们称其为最优子结构。

状态转移方程

状态转移方程也就是如何通过子问题的最优解得到总问题的最优解，这个求得解的方法，我们称其为状态转移方程。

重叠子问题

动态规划问题中往往存在重叠子问题，重叠子问题是在使用 普通的自顶向下 的方式（比如递归）来解决问题时，往往会花费重复的功夫来进行计算同一个问题。

为什么会存在重叠子问题呢？我认为根本原因是计算当前状态的最优值需要用到前面 多个状态 的最优值，所以导致解决不同问题需要用到同一个子问题的最优解。也就是这些前置状态出现了重合。当只需要一个子状态进行计算时，往往不会出现重合，所以重叠子问题多出现在子状态是多个的情况下。通俗来说，也就是状态转移方程等号右边多于一项的情况下。

如何思考动态规划问题

确定状态

状态，其实就是变量，其实就是要解决的问题中需要给出的可变的数值，其实就是提交后系统给出的不同的测试用例。

确定状态函数

得到状态后，我们需要确定关于状态的函数，也就是状态函数的定义，这个定义往往也是问题里就已经给出的。或者说，状态函数的定义其实就是 问题定义本身。

确定如何通过状态函数择优

知道了子问题的状态函数值，也就是最优值，那么如何得到总问题的状态函数值呢？这个过程也就是状态转移的过程，在这一步我们将确定状态转移函数。

明确边界条件

递归不能无穷进行下去，仅有状态转移方程也不够，我们还需要给出最小的子问题的值来驱动状态之间的转移。

动态规划的实现

自顶向下的实现

自顶向下更符合我们的逻辑流，但是会出现重叠子问题。为了避免其带来的性能开销，我们需要引入备忘录。

自底向上的实现

在某些情况下，可能可以省去备忘录带来的空间开销。

动态规划的变种

树形 DP

图 DP

动态规划刷题心得体会

• 可以使用多个状态转移函数，参考 买卖股票的最佳时机 III - 买卖股票的最佳时机 III - 力扣（LeetCode）。
• 最值问题可以用动规。

树

Trie 前缀树 / 字典树

有的人读作 tree，有的人读作 try。Trie 这个术语来自于 retrieval，也就是检索的意思。Trie 可以是多叉的。

与二叉查找树不同，键不是直接保存在节点中，而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀，也就是这个节点对应的字符串，而根节点对应空字符串。

字典树就是前缀树。下面这个图非常直观：

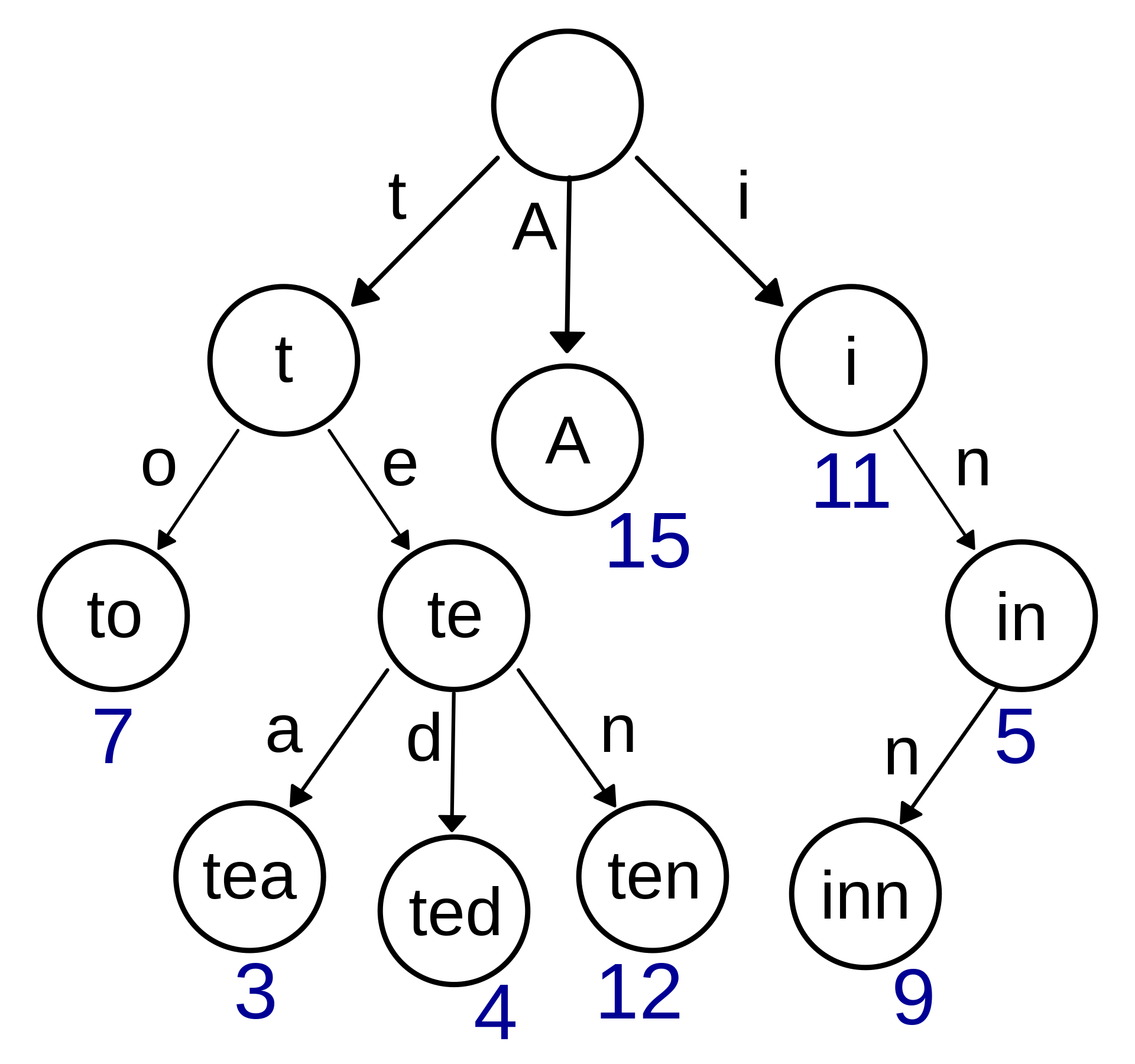
那么，这个树的应用场景一般在哪里呢？

Trie 树常用于搜索提示。如当输入一个网址，可以自动搜索出可能的选择。当没有完全匹配的搜索结果，可以返回前缀最相似的可能。

从这里 字典树 - 力扣（LeetCode）全球极客挚爱的技术成长平台 也可以看到，前缀树主要是用来做字符串匹配的。

二叉树刷题心得体会

• 二叉树大多都可以转化成为 分治问题，多思考在本节点应该做什么，如果思考不出来，那么可能就是 问题二叉树 的分治问题，也就是需要加入辅助函数，变化当前的状态参数（而不是只是把本节点作为状态参数），从而将当前的 表层二叉树 转化为深层的 问题二叉树 进行解决。
• 当题目提供的树的表示形式为边的列表时，可以通过邻接链表的形式来表示。
• 广度优先搜索可以使用列表 + 循环的方式实现，非常简单。

Radix Trie 基数树

从名字不难看出来，是字典树的一种。也叫压缩前缀树，是一种更节省空间的 Trie^。内核里一个 file 记录自己 page cache 里面所有 page 就用到了 radix trie 这个数据结构。

其中作为唯一子节点的每个节点都与其父节点合并：

回溯

如何思考回溯问题

需要思考三个问题，分别是：

• 路径：已经做出的选择；
• 选择列表：当前可以做的选择；
• 结束条件：到达决策树底层无需再进行选择的条件。

需要注意的是，回溯算法中不存在重叠子问题。

回溯算法的实现

基本框架

先来看看回溯算法最 基本 的代码框架：

def backtrack(路径, 选择列表): 
	for 选择 in 选择列表: 
		# 做选择（路径中添加我们的选择，计算新的路径列表）
		backtrack(路径, 选择列表) 
		# 撤销选择（路径中去除已经做的选择）

回想一下树（不只是二叉树）的遍历，通常有前序遍历、中序遍历（当为二叉树时）以及后序遍历。它们的代码是这样的：

def traverse(我):
	for 儿子 in 儿子列表:
		# 前序遍历需要的操作 
		traverse(儿子)
		# 后序遍历需要的操作

除了满足结束条件那里，其他的地方是不是很像？都是在递归之前可以执行操作（做选择、前序遍历），或者在递归之后可以执行操作（撤销选择、后续遍历）。

我们可以抽象一下这些操作，就会发现这些操作都是在进入子树以及退出子树时的操作。都是 得到状态 的操作。

遍历时因为树是 已经存在 的，所以我们需要通过诸如 root->val 的操作来访问这些节点的状态，通过通过前后来调整访问的时机。

回溯时因为树是 不存在 的，是虚构的，是抽象的，所以我们无法通过直接访问节点来得到状态，而需要通过手动构建来得到状态。那么如何进行手动构建呢？我们需要在进入时 做选择，来保持我们在树中节点的位置也就是状态的更新；同时，我们需要在出来时撤销选择，同样为了保持状态的同步。与遍历时节点的值不同，我们的状态是 路径 和 选择列表（很正常，因为我从哪来，以及到哪里去这两个位置就能够标识我的位置）。

加入结束条件

我们需要加入结束条件来判断是否触底，也就是到达了树的 最底层。

result = [] 
def backtrack(路径, 选择列表): 
	if 满⾜结束条件: 
		result.add(路径) 
		return
	for 选择 in 选择列表: 
		# 做选择（路径中添加我们的选择，计算新的路径列表）
		backtrack(路径, 选择列表) 
		# 撤销选择（路径中去除已经做的选择）

但是即使不判断结束条件，当触底时，选择列表为空，那么程序也会自动返回，那么为什么还要加入这一段代码呢？原因是 当触底时，我们需要判断得到的解是否是我们想要的解，所以我们需要添加这段代码。

加入剪枝

有时候为了加速计算过程，减少遍历带来的时间开销，我们可以加入剪枝：

result = [] 
def backtrack(路径, 选择列表): 
	if 满⾜结束条件: 
		result.add(路径) 
		return
	for 选择 in 选择列表: 
		# 做选择（路径中添加我们的选择，计算新的路径列表）
       if isNotValid(新路径，新的路径列表):
        	# 撤销选择（路径中去除已经做的选择）
       		continue
		backtrack(路径, 选择列表) 
		# 撤销选择（路径中去除已经做的选择）

只要一个答案

我们还没有利用函数的返回值信息，其实我们可以把这个看作是一种状态信息，代表有没有找到一个解，找到了就返回真，从而避免更多的搜索。

更新后的代码框架如下：

result = [] 
def backtrack(路径, 选择列表): 
	if 满⾜结束条件:
		result.add(路径) 
		return True;
	for 选择 in 选择列表: 
		# 做选择（路径中添加我们的选择，计算新的路径列表）
       if isNotValid(新路径，新的路径列表):
        	# 撤销选择（路径中去除已经做的选择）
       		continue
		if backtrack(路径, 选择列表):
       		return True
		# 撤销选择（路径中去除已经做的选择）
	return False;

BFS

BFS 的本质

问题的本质就是让你在⼀幅「图」中找到从** 起点到终点的最近距离**。

BFS 的核⼼思想不难理解，就是把⼀些问题抽象成图，从⼀个点开始，向四周开始扩散。⼀般来说，我们写 BFS 算法都是⽤「队列」这种数据结构，每次将⼀个节点周围的所有节点加⼊队列。

BFS 的框架

在 Python 中，我们可以通过一个 for 循环来模拟一个队列，比如对于二叉树的层序遍历，我们可以：

for node, level in nodes:
    if node.left:
        nodes.append((node.left, level + 1))
    if node.right:
        nodes.append((node.right, level + 1))

来快速地进行广度优先遍历。

import queue

# 计算从起点 start 到终点 target 的最近距离 
def BFS(start, target): 
    q = queue.Queue()
    visited = set() # 避免⾛回头路
    
    q.put(start); # 将起点加⼊队列 
    visited.add(start)
    step = 0 # 记录扩散的步数
    
    while not q.empty():
        sz = q.qsize()
        for i in range(sz):
            cur = q.get()
            if cur is target:
                return step
            
            for x in cur.adj():
                if x not in visited:
                    q.put(x)
                    visited.add(x)
        step += 1

双向 BFS

传统的 BFS 框架就是从起点开始向四周扩散，遇到终点时停⽌；⽽双向 BFS 则是从起点和终点同时开始扩散，当两边有交集的时候停⽌。

不过，双向 BFS 也有局限，因为你必须知道终点在哪⾥。双向 BFS 还是遵循 BFS 算法框架的，只是不再使⽤队列，⽽是使⽤ HashSet ⽅便快速判断两个集合是否有交集。

二分查找

二分查找分类

首先要明白二分查找的分类， 对于数列 [1,2,2,2,3]，目标 2 来说：

• 找到值：也就是索引为 2 的位置；
• 找到 左侧边界，也就是索引为 1 的位置；
• 找到 右侧边界，也就是索引为 3 的位置。

这三种类别都遵从以下的查找框架。

二分查找框架

找到值

找到值的一个粗略的框架如下：

int binarySearch(int[] nums, int target) {
    int left = 0, right = ...;

    while(...) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            ... // 找到了直接返回
        } else if (nums[mid] < target) {
            left = ...
        } else if (nums[mid] > target) {
            right = ...
        }
    }
    return ...; // 肯定是没找到
}

这个里面有 6 个带有省略号的位置，都是我们需要注意的细节：

1. int left = 0, right = …; 处的省略号应当是 nums.length - 1，因为我们希望在 闭区间 内进行搜索。
2. while(…) { 处的省略号为 left <= right，因为是闭区间，所以要保持等号，因为当两者相等时，[left, left] 内仍然有一个数需要被搜索。
3. 第一个判断应当返回 return mid; ，这是毋庸置疑的，因为判断成功了嘛。
4. left = mid + 1; 是因为 mid 处判断过了肯定不是，所以就从它的右侧开始。
5. right = mid - 1; 同理。
6. return -1; 表示什么都没有搜索到。

这样子很完美，唯一的缺点就是无法处理左侧边界和右侧边界情况。

左侧边界

以上提到的三种查找概念对应于下面三个框架，我会对此进行一一解释。

int left_bound(int[] nums, int target) {
    int left = 0, right = nums.length - 1; // 仍然是闭区间搜索
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1; // 根据终止条件，left是结果
        } else if (nums[mid] > target) {
            right = mid - 1;
        } else if (nums[mid] == target) {
            right = mid - 1; // 因为找左边界，所以把右边界往左跳
        }
    }
    // 防止left越界
    if (left >= nums.length || nums[left] != target)
        return -1;
    return left;
}

右侧边界

int right_bound(int[] nums, int target) {
    int left = 0, right = nums.length - 1; // 仍然是闭区间搜索
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        } else if (nums[mid] == target) {
            left = mid + 1; // 因为找右边界，所以把左边界往右跳
        }
    }
    // 防止right越界
    if (right < 0 || nums[right] != target)
        return -1;
    return right;
}

二分查找的变种

旋转排序数组

诀窍是只比较 start 和 mid 的值以进行分类：

• start 和 mid 值相等，毋庸置疑，存在值重复，去掉 start，start += 1；
• start < mid 值，start 到 mid 之间是有序的，此时判断 target 来决定取左还是取右；
• start > mid 值，mid 到 end 之间是有序的，此时同上。

滑动窗口算法

滑动窗口技巧是双指针技巧中最难掌握的一类。此算法的时间复杂度为 $O(n)$。

主要的框架是：

void slidingWindow(string s, string t) {
    unordered_map<char, int> need, window; // 目标内容和窗口里的内容
    for (char c : t) need[c]++;

    int left = 0, right = 0; // 与二分搜索不同，此区间是左闭右开的，[0,0)代表区间内没有任何元素
    int valid = 0; 
    while (right < s.size()) {
        char c = s[right];
        right++; // 右移窗口
        
        // I 扩张窗口数据更新

        printf("window: [%d, %d)\n", left, right); // debug

        // II 判断左侧窗口是否要收缩
        while (window needs shrink) {
            char d = s[left];
            left++; // 左移窗口
            
            // III 收缩窗口更新
        }
    }
}

适用场景

字符串相关

和字符串相关的题目可以考虑用滑动窗口能不能进行解决。

股票买卖系列问题

使用状态机来解决，状态机本身其实就是 DP Table。

并查集

使用 Python，并查集可以简单的使用一个列表来进行表示，其中列表的第 i 项表示第 i 个元素的父元素的下标。

# 初始化并查集列表（在刚开始，每一个元素的父节点都是它自己）
uf = [i for i in range(n)]

# 不断找，找到一个元素的根节点，添加了路径压缩
def find(p):
    # 首先找到根节点
    r = p
    while uf[p] != p:
        p = uf[p]
        
    # 把所有遍历到的元素全部指向根节点
    while r != p:
        uf[r], r = p, uf[r]
    return p

def connected(p, q):
    return find(p) == find(q)

def merge(p, q):
    root_p, root_q = find(p), find(q)
    if root_p != root_q:
        if[root_p] = root_q

数学

将一根木棍分成三段，求这三段构成三角形概率

使用可行域法。

将一根木棍分成三段，求这三段构成三角形的概率_退而结网-CSDN博客_一根木棒截成三段,能组成三角形的概率

均匀分布求 max 期望

均匀分布max函数期望_若随机变量X和Y相互独立且服从[0,1]上的均匀分布,则Z=max{X,Y}的期望E(Z)=_三人行教育网_www.3rxing.org

最大公约数、最小公倍数

两个数之间求最大公约数。使用欧几里得算法，也就是辗转相除法。

多个数之间求最大公约数。首先求出前两个数的最大公约数，求出之后再求此数与后一个数的最大公约数，由此递归执行可以得到一个数组的最大公约数。

两个数组，分别从这两个数组里选择一个数求它们的最大公约数，求所有可能的最大公约数当中的最大值。

质因数分解

评论里的答案才是正解，不需要枚举每一个质数，枚举每一个数就可以了。

入门算法 - 质因数分解 - 简书

除法

整数除法，不能使用乘除以及模。

可以使用倍增法，比如 11 除以 2，11 > 2，然后将 2 翻倍得到 4，11 > 4，然后将 4 翻倍得到 8，11 > 8，然后将 8 翻倍得到 16，发现不等式不满足了，那就只能 11 - 8 = 3 再算这个数和 2 的商了。

其他

计算器

使用双栈，一个保存操作数，另一个保存操作符。

诀窍在于：当前字符为数字时，把完整的数识别出来放到栈中；当前为操作符时，根据优先级计算栈中之前已经保存的优先级大于此操作符的操作符。

计算器相关题目如下：

• 224. 基本计算器 - 力扣（LeetCode）
• 227. 基本计算器 II - 力扣（LeetCode）
• 772
• 770. 基本计算器 IV - 力扣（LeetCode）

旋转矩阵

模拟题，不费脑子，但是比较麻烦。

class Solution:
    def generateMatrix(self, n: int) -> List[List[int]]:
        l, r, t, b = 0, n - 1, 0, n - 1
        mat = [[0 for _ in range(n)] for _ in range(n)]
        num, tar = 1, n * n
        while num <= tar:
            for i in range(l, r + 1):
                mat[t][i] = num
                num += 1
            for i in range(t + 1, b + 1):
                mat[i][r] = num
                num += 1
            for i in range(r - 1, l - 1, -1):
                mat[b][i] = num
                num += 1
            for i in range(b - 1, t, -1):
                mat[i][l] = num
                num += 1
            l += 1
            r -= 1
            t += 1
            b -= 1
        return mat

Python 刷题必备

队列、双端队列

使用 collections.deque, 默认实现是一个栈。左端插入使用 appendleft，右端插入使用 append，左端删除使用 popleft，右端删除使用 pop。

有序字典

基于 Key 排序的字典用 collections.OrderedDict()。

基于 Value 排序的字典暂时还没有用到。

字典

默认字典用 collections.defaultdict(int/list/set) 等等。或者 collections.defaultdict(lambda: []) 等等。

处理输入输出

ACM输入输出之python - starry_sky - 博客园

字符串

'<string>'.find() 可以返回下标

三角函数

math.sin(), math.cos(), math.tan(), math.asin(), math.acos(), math.atan(), math.degrees(), math.radians()。

Python 里的队列

使用列表即可，加入元素用 append()，出元素用 pop(0)。广度优先搜索因为可以用队列实现，而在 python 当中直接使用 for 循环对一个队列遍历其实就是广搜。

Python 里的栈

使用列表即可，加入元素用 append()，出元素用 pop()。

固定保留小数点位输出

print("%.2f" % num)

Python 里的堆

首先要 import heapq：

• 堆化使用 heapq.heapify(heap)；
• 取出元素用 heapq.heappop(heap)；
• 放入元素用 heapq.heappush(heap, val)；
• 取出一个的同时放入一个用 heapq.heappushpop(heap, val)，能够保证堆的大小是不变的。
• 默认是小根堆。

固定大小的堆可以这么用：

if len(h) < capacity:
    heapq.heappush(h, thing)
else:
    # Equivalent to a push, then a pop, but faster
    spilled_value = heapq.heappushpop(h, thing)
    do_whatever_with(spilled_value)

如果不能用 Python 里自己带的堆实现的话，可以使用下面的这个轮子：

class MinHeap():
    def __init__(self, maxSize=None):
        self.maxSize = maxSize 
        self.array = [None] * maxSize 
        self._count = 0
    
    def __len__(self):
        return self._count 
    
    def push(self, value):
        self.array[self._count] = value
        self._shift_up(self._count)
        self._count += 1
    
    def _shift_up(self, index):
        if index > 0:
            parent = (index - 1) // 2
            if self.array[parent] > self.array[index]:
                self.array[parent], self.array[index] = self.array[index], self.array[parent]
                self._shift_up(parent)
    
    def pop(self):           
        value = self.array[0]

        self._count -= 1
        self.array[0] = self.array[self._count]
        self._shift_down(0)
        
        return value 
             
    def _shift_down(self, index):  
        if index < self._count:
            left = 2 * index + 1
            right = 2 * index + 2
            # 左右子节点都有的情况
            if left < self._count and right < self._count:
                if self.array[left] < self.array[index] and self.array[left] < self.array[right]:
                    self.array[index], self.array[left] = self.array[left], self.array[index] #交换得到较小的值
                    self._shift_down(left)
                elif and self.array[right] < self.array[left] and self.array[right] < self.array[index]:
                    self.array[right], self.array[index] = self.array[index], self.array[right]
                    self._shift_down(right)
            # 只有左子节点，没有右子节点的情况
            elif left < self._count and right > self._count and self.array[left] < self.array[index]:
                self.array[left], self.array[index] = self.array[index], self.array[left]
                self._shift_down(left)

Python 输入输出

输入有多行，每一行有多个数字可以像下图这样进行处理：

line = input()
while line:
    # process input
    # ...
    line = input()
# do something and print...

Tricks

判断一个数是否前面全是 1 后面全是 0，比如子网掩码

if ~(num | (num - 1)):
    return False
else:
    return True

前缀和（通常和哈希表、二分查找一起使用）

560. 和为K的子数组 - 力扣（LeetCode）

前缀和＋哈希表能够得到 $O(n)$ 的时间复杂度。

523. 连续的子数组和 - 力扣（LeetCode）

前缀和＋哈希表。

525. 连续数组 - 力扣（LeetCode）

前缀和＋哈希表。

原地哈希

41. 缺失的第一个正数 - 力扣（LeetCode）

如果可以使用 $O(n)$ 的空间复杂度，那么我们可以重新开一个列表，记录这个数是否出现。

如果需要常数的时间复杂度，那么我们需要把标记设计成负号。

多源 BFS

542. 01 矩阵 - 力扣（LeetCode）

最值维护

如何解决 O(1) 复杂度的 API 设计题 - 队列的最大值 - 力扣（LeetCode）

在滑动窗口的过程中如何维护最小值与最大值？

使用两个双端队列，一个 queue 用来存所有的值，一个 max_val 用来存最值。

当加入新的元素时：

• queue 当中直接加入即可
• max_val 需要以单调栈的形式加入，注意只弹出严格小于的，等于的不需要弹。

当弹出新的元素时：

• queue 当中可以直接弹出
• max_val 需要进行对比，如果相等的话就可以弹出

快慢/先后指针/滑动窗口

滑动窗口 = 先后指针 = 双指针。

本质上是一个队列，左边出，右边进。

单调栈

496. 下一个更大元素 I - 力扣（LeetCode）

84. 柱状图中最大的矩形 题解 - 力扣（LeetCode）

1130. 叶值的最小代价生成树 - 力扣（LeetCode）

122. 买卖股票的最佳时机 II - 力扣（LeetCode）

状态的精细保持

1038. 把二叉搜索树转换为累加树 - 力扣（LeetCode）

109. 有序链表转换二叉搜索树 - 力扣（LeetCode）

异或

137. 只出现一次的数字 II - 力扣（LeetCode）

线段树

字典树

脑筋急转弯

260. 只出现一次的数字 III - 力扣（LeetCode）

如果只有一个数字出现了一次，那么我们知道怎么处理，就是异或。

现在有两个数字只出现了一次，如果我们可以分组，把这两个数字分在不同的两组，然后组内其他数字都出现了两次，那么我们就可以把问题转化为只有一个数字出现一次的问题。

我们先进行全异或，找到为 1 的位，按此位对数字进行分组就可。

KMP 算法

字符串匹配算法。核心思想是一个 next 数组。要将子串匹配母串。

利用的是这一特性：在子串已经匹配的序列 a 中，我们可以找到一个字符串 b，其既是 a 的前缀也是 a 的后缀。并且 b 应该是所有满足条件的串里最长的。只有同时是前缀也是后缀，我们才能向后移动这个串的长度。

next[i] 表示的是该下标一旦和母串没有匹配，应该跳到哪里进行匹配。

我们可以把匹配的过程看作母串中匹配的位置 i 在每一轮固定，子串不断向右跳，也就是子串匹配位置 j 不断向左移动的过程。